Nella precedente lezione abbiamo introdotto le disposizioni semplici prendendo come esempio l’estrazione di oggetti distinti tra loro da una scatola. Ora ci occuperemo di un problema simile che ci porterà alla definizione delle disposizioni con ripetizione.
DEFINIZIONE DI DISPOSIZIONE CON RIPETIZIONE
Come fatto per le disposizioni semplici andiamo a considerare un situazione ideale. Immaginiamo di voler estrarre da una scatola degli oggetti diversi tra loro prendendo nota del loro ordine di estrazione stilando una lista. Introduciamo in questo caso una modifica, infatti dopo aver estratto un oggetto e averne preso nota lo andremo a reinserire nella scatola.
Come possiamo ben immaginare questa modifica fa si che un qualsiasi oggetto dentro la scatola possa essere estratto più di una volta. Il numero di oggetti all’interno della scatola, a differenza di quanto accade per le disposizione semplici, rimane lo stesso perché dopo ogni estrazione l’oggetto viene reinserito.
Essendo che un oggetto può essere preso più volte, la lista ordinata potrà avere degli elementi che si ripetono, sarà quindi una disposizione con ripetizione.
Quello che ci interessa sarà quante sono le disposizioni (con ripetizione) che possiamo estrarre e qual è la formula per calcolarle.
Vediamo quindi la definizione formale disposizione con ripetizioni e la formula che permette di calcolare il numero totale di disposizioni con ripetizione possibili.
Dati $n$ elementi distinti, le disposizioni con ripetizione di ordine $k$ (con $k\in \mathbb{N}$) sono tutti i gruppi di $k$ elementi presi dagli $n$, anche ripetuti, che differiscono tra loro o per almeno un elemento o per l’ordine con cui vengono scelti. Dati $n$ e $k$ il numero di disposizioni con ripetizione $D’_{n,k}$ è dato dalla formula: $D’_{n,k}=n^k$
Facciamo alcune osservazioni sulla definizione appena vista:
- gli $n$ elementi di partenza devono essere distinti tra loro, ossia tutti diversi
- $k,n \in \mathbb{N}$
- due disposizioni sono diverse se hanno almeno un elemento diverso tra loro o se contengono gli stessi elementi questi devono avere ordine diverso
Ciò che differisce le disposizioni semplici da quelle con ripetizione, oltre al fatto che gli elementi possono ripetersi all’interno di una singola disposizione, sta nel valore di $k$. Il numero $k$ indica di quanti elementi è formata la disposizione, se nelle disposizioni semplici doveva rispettare la condizione $k \le n$ (cioè $1\le k \le n$), nelle disposizioni con ripetizione $k$ non ha alcuna condizione e può essere un numero naturale qualsiasi (anche maggiore di $n$).
Questo fatto è dovuto alla possibilità di ripetere quante volte vogliamo lo stesso elemento all’interno di una disposizione. Nelle disposizioni semplici invece tutti gli elementi “estratti” devono essere diversi tra loro e una volta finiti gli $n$ elementi a disposizione non si può andare oltre.
Chiariamo quanto visto con un esempio.
ESEMPIO
Un dado viene lanciato due volte, calcola quanti sono i possibili risultati.
Per risolvere l’esercizio andiamo come prima cosa a scrivere qual è l’insieme degli $n$ elementi di partenza. Nel nostro caso abbiamo che i possibili elementi sono le facce numerate del dado, quindi abbiamo sei elementi di partenza ($n=6$) e l’insieme di partenza sarà $A=\{1,2,3,4,5,6\}$.
I risultati saranno delle coppie di numeri $(a,b)$, l’elemento $a$ della coppia sarà il numero della faccia uscita al primo lancio mentre l’elemento $b$ sarà il numero uscito al secondo lancio.
Ovviamente facendo due lanci del dado ($k=2$), c’è la possibilità di ottenere due volte lo stesso numero (cioè lo stesso elemento) quindi otteniamo delle disposizioni con ripetizione.
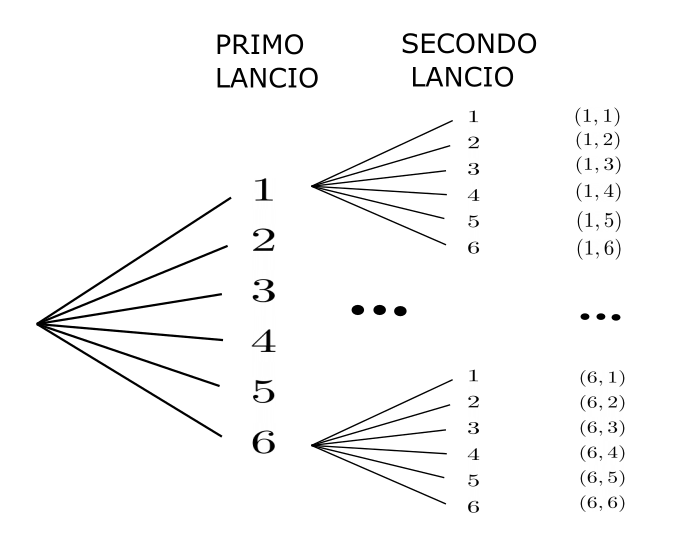
Ora che abbiamo identificato le caratteristiche del problema (elementi distinti e ripetibili) e che abbiamo definito il valore di $k$ ed $n$ possiamo applicare la formula per il calcolo del numero di disposizioni con ripetizione:
$D’_{n,k}=n^k$
che inserendo i valori del problema diventa:
$D’_{6,2}=6^2=36$
Abbiamo quindi $36$ possibili risultati differenti.
Vediamo un ulteriore esempio:
Quante parole di $5$ lettere è possibile scrivere con le $21$ lettere dell’alfabeto?
Stiamo considerando come insieme di partenza l’insieme delle lettere dell’alfabeto italiano $A=\{a,b,c,d,e,f,…\}$ che come suggerisce l’esercizio sono $21$. Dobbiamo capire quante parole (anche prive di significato) è possibile formare prendendo $5$ elementi da $A$.
Siccome il problema non lo specifica assumiamo che gli elementi possano essere usati più volte. Ovviamente l’ordine è importante, ad esempio la parola “$cddas$” e la parola “$sadcd$” hanno gli stessi elementi ma avendo il loro ordine scambiato sono considerate due parole distinte.
Essendo importante l’ordine possiamo considerare le parole come delle disposizioni con ripetizione di ordine $k=5$ di un insieme di $n=21$ elementi. Andiamo quindi ad utilizzare la formula per calcolare quante sono le disposizioni con ripetizione possibili dati $k=5$ ed $n=21$.
$D’_{21,5}=21^5=4084101$
Quindi con $21$ lettere è possibile formare $4084101$ parole di $5$ lettere.
Esercizi svolti su disposizioni con ripetizione? Ecco QUI