Problema
Risolvere le seguenti equivalenze tra aree:
$0,003dm^2=…cm^2$
$11,7m^2=…hm^2$
$310mm^2=…dam^2$
$0,433km^2=…m^2$
Svolgimento
Per svolgere le equivalenze proposte partiamo dalla “scaletta” con multipli e sottomultipli delle unità di misura dell’area.
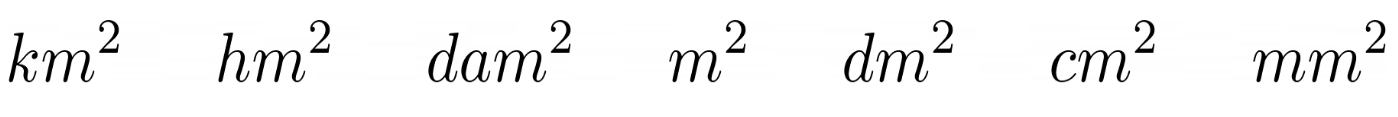
In questo caso ogni “salto” da sinistra verso destra corrisponde ad una moltiplicazione $\cdot 100$ mentre un salto da destra verso sinistra corrisponde ad una divisione $:100$.
Partendo da ciò iniziamo a risolvere le equivalenze dell’esercizio.
La prima equivalenza è la seguente $0,003dm^2=…cm^2$ e per risolverla andiamo a rappresentare sulla scaletta delle unità di misura i “salti” che separano i $dm^2$ dai $cm^2$. Otteniamo il seguente schema:

Quindi per risolvere l’equivalenza andiamo a moltiplicare $\cdot 100$ il valore numerico di partenza:
$0,003dm^2=(0,003\cdot 100)cm^2=0,3cm^2$
La seconda equivalenza da risolvere è $11,7m^2=…hm^2$ che calcoleremo utilizzando lo stesso procedimento appena visto:

Quindi l’operazione da effettuare è una doppia divisione $:100$, cioè una divisione $:10000$, da cui otteniamo:
$11,7m^2=(11,7:10000)hm^2=0,00117hm^2$
Passiamo alla terza equivalenza $310mm^2=…dam^2$

Per risolvere l’equivalenza dobbiamo dividere quattro volte per $100$, ossia dividere per $:100000000$:
$310mm^2=(310:100000000)dam^2=0,00000310dam^2$
La quarta equivalenza è $0,433km^2=…m^2$

Quindi andiamo a moltiplicare $\cdot 1000000$, otteniamo cioè:
$0,433km^2=(0,433\cdot 1000000)m^2=433000m^2$